Covid-19: qualche dato

Data Analysis · 16 Mar 2020

In questi giorni l'attenzione di tutti è per il virus SARS-CoV-2, comunemente chiamato "Coronavirus". Esso è stato individuato per la prima volta nella città di Wuhan in Cina il 31-12-2019 e ha avuto una rapida diffusione (guarda la cronistoria).

Il Virus

Il Coronavirus si è diffuso subito in molti paesi, tra cui l'Italia, creando non pochi problemi e costringendo i governi a varare misure eccezionali per cercare di contenere la sua diffusione e non gravare sui vari sistemi sanitari. In questo post si cercherà di spiegare, utilizzando modelli matematici, come si diffonde un virus e perchè il virus Sars-CoV-2 è "pericoloso" per il SSN Italiano. Infine commenteremo qualche dato per comprendere la motivaione delle misure di contenimento prese dal Governo Italiano.

Il Modello SIR

L'Epidemiologia, cioè la scienza che studia la diffusione delle epidemie, ha sviluppato dei modelli matematico-computazionali per cercare di studiare l'andamento e prevedere parametri importanti nella diffusione delle epidemie. Uno di questi modelli è il SIR, acronimo di Susceptible-Infected-Recovered (Suscettibili-Infetti-Recuperati). Questo modello, introdotto da Kermack and McKendrick nel 1927, è un cosiddetto modello compartimentale poichè suddivide la popolazione in tre compartimenti (S, I, ed R) e simula cosa potrebbe succedere, col passare del tempo, agli individui appartententi a queste popolazioni. Come ogni modello, esso cerca di descrivere la realtà, partendo da alcune ipotesi iniziali), ma non è la realtà. Ciò che accade realmente è molto complesso e occorre comprendere che, pur essendo questo modello una buona approssimazione, esso non è esatto. Per chi fosse curioso, le equazioni che descrivono il modello SIR sono riportate di seguito: \[{dS \over dt} = -\beta SI ~~~~~(1)\] \[{dI \over dt} = \beta SI + \gamma I ~~~(2)\] \[{dR \over dt} = \gamma I ~~~~~(3)\] Tali equazioni sono equazioni differenziali. Come equazioni esprimono l'idea di uguaglianza tra che ciò che si trova a sinistra e ciò che si trova a destra del simbolo "=". Le equazioni differenziali "descrivono" la variazione di una quantità rispetto ad un'altra. A sinistra del simbolo "=" abbiamo i d/dt che leggeremo come "la variazione nel tempo di S (1), I (2) ed R (3) rispettivamente. A destra del simbolo "=" abbiamo moltiplicazioni, somme e sottrazioni. La prima equazione si legge "la variazione nel tempo dei Suscettibili è uguale all'opposto del prodotto tra β, i Suscettibili ed gli Infetti. I simboli β e γ sono i cosiddetti parametri del modello: rappresentano rispettivamente il parametro di trasmissione (tasso di contagio tra persone S e I) e il parametro di recuperati (tasso di persone passate da I a R). La quantità R₀ = β/γ è chiamata numero di riproduzione di base: rappresenta il numero medio di infezioni secondarie, ovvero quelle prodotte da ciascun individuo infetto in una popolazione completamente suscettibile (mai venuta a contatto con il nuovo patogeno emergente). Questo parametro misura la potenziale trasmissibilità di una malattia infettiva. Quanto maggiore è il valore di R₀, tanto più elevato è il rischio di diffusione dell’epidemia. Se il fattore R₀ di una malattia infettiva è circa 2, significa che -in media- un singolo malato infetterà due persone. Se invece il valore di R₀ è inferiore ad 1 significa che -in media- un singolo malato infetterà "meno di una persona" e dunque l’epidemia può essere contenuta. Implementando il modello e simulando al computer la sua dinamica (la sua evoluzione nel tempo con dei valori fittizi), quello che otteniamo è un grafico tipo quello in Fig.1

Fig.1 - Simulazione del Modello SIR utilizzando parametri fittizi.

Le curve indicano, al passare del tempo, la percentuale di individui che appartengono ad ogni compartimento. Descriviamo la curva rossa (quella degli Infetti): essa raggiunge un picco e poi decade. Tale picco è più o meno alto e più o meno traslato nel tempo, a seconda dei parametri β e γ.

Perchè il picco è importante?

Il picco è una caratteristica da tenere in considerazione: rappresenta il numero massimo di Infetti in un giorno. La Fig.2 compara due casi:

curva rossa: la diffusione dell'epidemia è veloce e si ha un picco molto alto e "vicino nel tempo";
curva blu: la diffusione dell'epidemia è meno veloce e si ha un picco più basso e più "lontano nel tempo"

In Fig.2, inoltre, si può vedere una linea orizzontale nera: questa rappresenta la capacità di posti in terapia intensiva del SSN. Come riportato nelle statistiche, nel caso specifico del SARS-CoV-2, circa un 11% di Infetti sviluppa delle complicazioni tali per cui è necessario un ricovero in terapia intensiva. Conoscere il picco di contagi aiuterebbe a stimare quante persone potrebbero aver bisogno della terapia intensiva. Confrontando questo con il numero effettivo dei posti disponibili in terapia intensiva si potrebbe stimare se il SSN collasserebbe oppure riuscirebbe a far fronte all'avanzata dell'epidemia. In Fig.2 le curve arancione e celeste rappresentano l'11% degli Infetti rispettivamente nel primo (curva rossa) e nel secondo caso (curva blu) di epidemia. Come si può notare, nel primo caso il SSN non riuscirebbe a far fronte al numero dei ricoveri in terapia intensiva: la curva arancione è nel momento del picco sopra la curva nera. Nel secondo caso il SSN riuscirebbe a sistemare tutti i pazienti in terapia intensiva: la curva celeste è al di sotto della curva nera.

Fig.2 - Andamento degli Infetti in due scenari diversi.

La domanda che occorrerebbe porsi è "come si può passare dalla curva rossa alla curva blu, dando quindi tempo al SSN di assorbire i casi acuti?" La Matematica (e il modello SIR), risponde con la NECESSITA' di ridurre il valore del coefficiente β. In pratica è necessario ridurre il tasso di contagio EVITANDO I CONTATTI CON ALTRE PERSONE: SEMPLICEMENTE STANDO A CASA E USANDO MISURE PROTETTIVE. Stare TUTTI (non solo i malati) a casa si rende necessario in quanto la maggior parte dei contagiati dal virus è asintomatico (non mostra i sintomi e non sa di essere malato), ma può infettare gli altri. Limitare i contatti serve soprattuto ad evitare che gli asintomatici possano infettare le persone con cui vengono a contatto. Proprio per questo motivo il Governo ha varato delle misure che potrebbero essere definite di "allontanamento sociale" (la sospensione di aggregazioni pubbliche e dei trasporti ...) e di "riduzione della trasmissione per contatto" (ad es. mediante l'uso di misure di protezione personale). In Cina sembrerebbe che tali misure riducano numero di riproduzione di base R₀, agendo sul coefficiente β.

Qual è la situazione Italiana?

Per comprendere la situazione Italiana possiamo leggere i dati reali (disponibili sul sito della protezione civile ) e possiamo fare una simulazione utilizzando il modello SIR (stimado i valori β e γ).

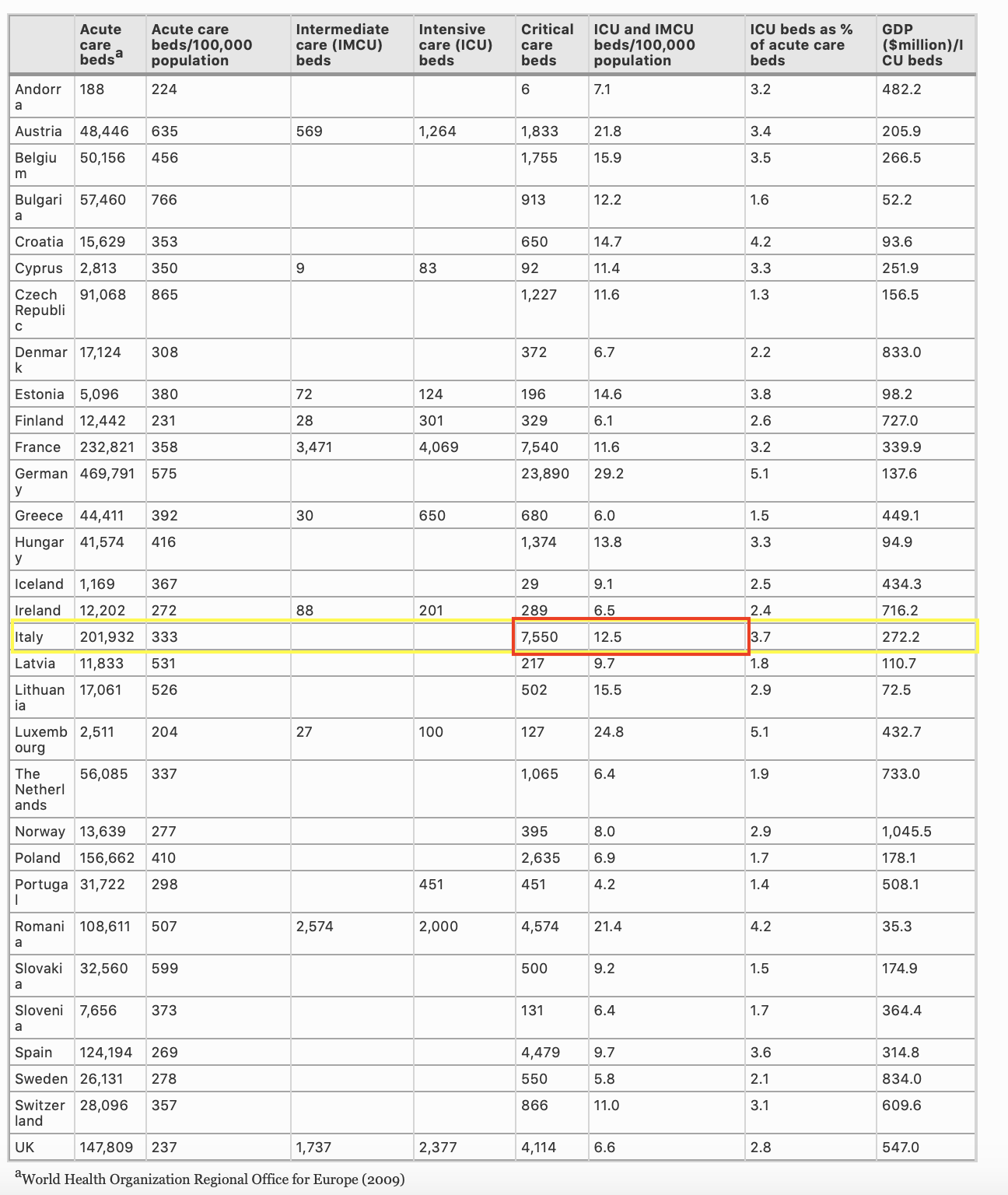
Il primo dato (reale) che ci occorre conoscere è quello che descrive il numero dei posti letto in terapia intensiva. In Fig.3 è riportata una tabella presa dall'articolo The variability of critical care bed numbers in Europe (di Rhodes et all.) apparso nel 2012 nella rivista Intensive Care Medicine. Dall’articolo si evince che al 2009 il numero di posti in terapia intesiva (ICU and IMCU beds) è di 12.5 ogni 100000 abitanti. Calcolando tale numero per l’intera popolazione italiana (60 milioni di abitanti) abbiamo, in totale, circa 7500 posti letto in terapia intensiva.

WHO — *Fig.3 - Tabella che descrive il numero dei posti letto nei paesi europei (dati Organizzazione Mandiale dellea Sanità).*

Occorre poi conoscere il valore di R₀, da cui ricaveremo β e γ. Da quando il Coronavirus, SARS-CoV-2, ha iniziato a diffondersi l'Organizzazion Mondiale della Sanità (OMS) e altri istituti di ricerca hanno diffuso stime di R₀. I valori di R₀ vanno da 1.4 a 3.8. Nella nostra simulazione si è deciso di usare il caso "peggiore", ovvero R₀=3.8. Dal momento che γ = 1/14 (14 sono i giorni in cui una persona infetta può infettare altri, al passare dei 14 giorni la persona viene definita recuperata) otteniamo che R₀*γ = β, quindi β=3.8/14 = 0.271. Utilizzando questi valori nel modello SIR, otteniamo l'andamento della Fig.4:

Fig.4 - Simulazione del modello con parametri "reali". Questo scenario è quello che potrebbe accadere in Italia.

Descriviamo il grafico in figura:

curva blu: la popolazione totale, che può essere infettata;
curva verde: la popolazione che non è più infetta;
curva rossa: la popolazione infetta e che può infettare gli altri;
curva arancione: la popolazione infetta, che può infettare gli altri e che richiede cure in terapia intensiva;
curva nera: posti disponibili in terapia intensiva.

Notiamo che la curva nera è notevolmente sotto la curva arancione: questo indica che i posti in terapia intensiva non riusciranno a soddisfare il bisogno dei pazienti.

I dati che leggiamo risultano particolarmente allarmanti e catastrofici. Dobbiamo però tener conto di alcune riflessioni:

il valore R₀ è solo una stima (l'esatto valore si conocerà solo alla fine dell'epidemia) e descrive la realtà cinese (che potrebbe essere differente da quella italiana);
in questa simulazione non si sta tenendo conto delle misure di contenimento che, come abbiamo visto in Fig.2, abbassano e "rallentano" il picco;
è probabile che il virus stia circolando in Italia da molto tempo (inizi/metà gennaio); se ciò fosse vero potrebbero esserci stati degli effetti di immunizzazione sulla popolazione di cui non siamo a conoscenza, che potrebbero abbassare ulteriormente il picco degli Infetti.

Cosa fare? Niente panico, ma evitate i contatti!

Le politiche di contenimento funzionano?

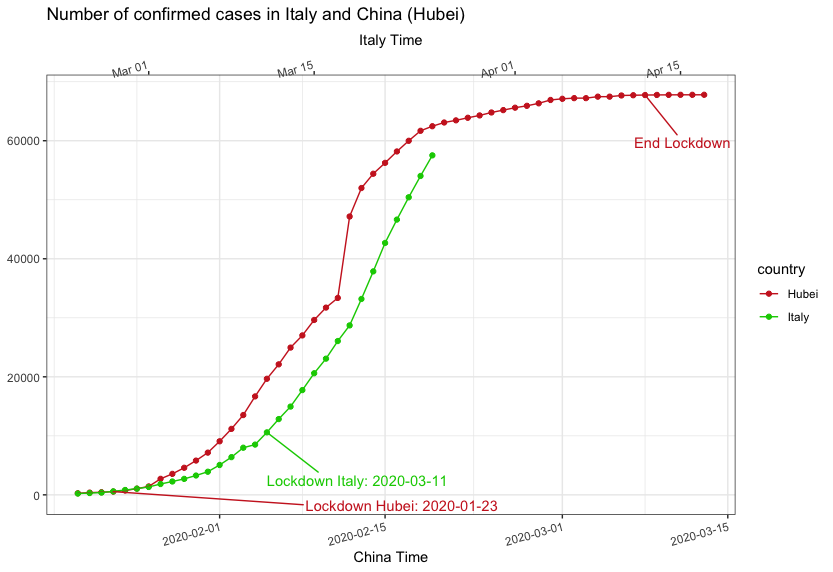
Per comprendere se le politiche di contenimento e di allontanamento sociale funzionino è necessario "leggere" cosa dicono i dati reali. In Fig. 5 sono mostrate due curve che rappresentano l'andamento dei nuovi contagi giornalieri nella Provincia di Hubei (curva rossa) e in Italia (curva verde). La provincia di Hubei, dove si trova Wuhan, ha circa la stessa popolazione dell'Italia: confrontare queste due realtà è più coerente che confrontare tutta la Cina con l'Italia. Le due curve sono allineate: partono entrambe dal giorno in cui i dati sono stati confermati dai rispettivi organismi ufficiali (20 Gennaio 2020 per la Cina e 24 Febbraio 2020 per l'Italia). Bisosogna dire, però, che i primi contagi in entrambi i paesi sono avvenuti almeno un mese prima di tali date. L'asse dei tempi per la Cina è in basso, mentre per l'Italia è in alto. Entrambe le curve riportano i dati fino al 14 Marzo 2020. Nella Fig.5 sono riportate anche l'inizio delle misure di contenimento (Lockdown) prese dai due Governi: il Governo Italiano è intervenuto quando la curva stava già assumendo un andamento esponenziale. Dopo 35 giorni di misure di contenimento, fonti NON ufficiali dichiarano che le misure siano state allentate. Notiamo che la curva della della provincia di Hubei sta arrivando a saturazione: non cresce/decresce e si sta mantenendo costante. Questo comportamento si discosta un po' dal modello teorico (SIR) dove il picco è netto ed è seguito da una riduzione dei contagiati. La differenza tra teoria e realtà potrebbe essere dovuta a diversi fattori fattori pratici nel procedimemto di processamento dei dati ed anche al fatto che i 14 giorni di infettività sono, in realtà, una media.

Lockdown_tot — *Fig.5 - Andamento dei nuovi contagi giornalieri nella Provincia di Hubei e in Italia* .

Guardiamo solo la situazione Italiana e facciamo riferimento alla Fig.6. Qui sono presenti dei pallini neri, che rappresentano i dati reali dei nuovi contagi cumulati giornalieri, e due curve: una arancione ed una blu. La curva blu rappresenta l'andamento dai dati, approssimato con una curva esponenziale (il fit), fino al giorno in cui il Governo Italiano non ha decretato le misure di contenimento (Lockdown); la curva arancione rappresenta l'andamento dei dati comprende il fit dei dati considerando anche i giorni successivi all'emanazione del decreto e fino al 15/03/2020. La curva verde rappresenta la stessa situazione della curva arancione ma fino al 17/03/2020. La differenza tra curva arancione e quella blu è mininima, tuttavia notiamo due pendenze diverse. Si può notare che c'è sato un effettivo (anche se minimo) rallentamento nelle previsioni degli Infetti; se guardiamo la curva verde, questa ha una pendenza minore sia della curva blue che della curva arancione indicando ancora un abbassamento del nuemero di Infetti. Bisogna continuare a favorire questa tendenza.

Oggi, 8 Aprile, si può vedere che i modelli esponenziali (curve blu, arancione, verde, giallo e celeste) usati inizialmente per descrivere i dati non riescono più a descriverli in maniera soddisfacente (curva marrone). Questo ha determinato la scelta di un modello diverso: si sono scelti un modello gaussiano (curva a campana), rappresentato dalla curva rosa, e un modello logistico (o curva sigmoide), rappresentato dalla curva viola. Si nota subito che il modello logistico è quello che descive meglio i dati raccolti fino a questo punto. Il modello logistico è descritto da una curva che ad un certo punto arriva ad un valore costante e anche se la variabile sull'asse orizzontale crcesce, ad esempio il tempo, la corrispondente valore sull'asse y non aumenta. Questa andamento è, teoricamente, in linea con quello che ci aspetteremmo di vedere: molto semplicemente significa che abbiamo raggiunto una situazione per cui tutti i soggetti infettabili sono stati infettati e quindi, non essendoci più nessuno suscettibile, il fenomeno epidemico è destinato ad estenguersi. E' importante ribadire che i dati descrivono i nuovi contagi cumalati giornaliere e quindi non si vedrà mai questi dati andare a zero. Ma vedendo i dati si potrebbe capire che non ci sono più nuovi conatagi quando il numero dei nuovi contagiati rimarrà costante per un determinato periodo (lungo) di tempo. Ovviamente la curva sigmoide potrebbe raggiungere la situazione stazionaria, ovvero di "non crescita", molto lentamente. Purtroppo questa tendenza potrebbe non essere quella effettiva poichè come si sa il munero degli infetti dipende abbastanza fortemente dal numero dei tamponi (pochi) che vengono effettuati e quindi i contagi che risultano dai dati potrebbero essere (anzi sono) sottostimati.

Fig.6 - andamento dei nuovi contagi giornalieri nella Provincia di Hubei e in Italia .

Per concludere si può affermare che:

i modelli mostrano che il SSN potrebbe essere messo a dura prova dal SARS-CoV-2;
i dati confermano l'aumento dei casi giornalieri e provano che il picco dei casi italiani deve ancora arrivare (probabilmente entro metà Aprile);
i dati mostrano che, dall'entrata in vigore dalle misure di "isolamento sociale", si è rilevata una lieve riduzione della velocità dei contagi ma solo nei prossimi si potrà determinare se tali misure hanno avuto realmente effetto; ora possiamo dire che qualcoso sta cambiando, ma bisogna essere consapevoli delle stime (a ribasso) del numero degli infetti.
rimanere a casa, evitare i contatti ed usare sturmenti di protezione erano le strategie da perseguire per ottenere un abbassamento del numero R₀, e quindi un abbassamento della velocità di crescita delle curve blu, giallo, arancione, verde e celeste in Fig.6, al fine di limitare e rallentare il contagio.
rimanere a casa il più possibile, evitare i contatti ed usare sturmenti di protezione è la strategia che si dovrebbe continuare ad usare per permettre alla curva viola di raggiungere la stazionarietà in manierà più veloce possibile.

(Aggiornato al 8/04/2020) In aggiornamento...

Marco Piangerelli e Renato De Leone